تبادل لینک هوشمند 
سری فوریه، روشی در ریاضیات میباشد که به وسیله آن، هر تابع متناوبی به صورت جمعی از توابع سینوس و کسینوس می‌تواند نوشته شود. نام این قضیه به اسم ریاضیدان فرانسوی، ژوزف فوریه ثبت شده است. هدف از این کار، نمایش توابع در دامنه فرکانس میباشد.
محتویات[نهفتن] |
[ویرایش] پیش گفتار
توابع مورد استفاده در مهندسی و توابع نمایانگر سیگنال‌ها معمولاً توابعی از زمان هستند یا به عبارت دیگر توابعی که در میدان زمان تعریف شده اند. برای حل بسیاری از مسائل بهتر است که تابع در دامنه فرکانس تعریف شده باشد زیرا این دامنه ویژگی‌هایی دارد که به راحتی محاسبات می‌انجامد.
فرض کنید که تابعی به شکل زیر تعریف شده است:
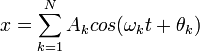
که در آن N یک عدد صحیح مثبت، Ak دامنه ، ωk فرکانس و θk فاز توابع کسینوسی میباشد. قابل مشاهده است که با در دست داشتن فرکانس‌ها 
، دامنه‌ها 
و فازها 
تابع یه طور کامل قابل تعریف است. توجه شود که بر این اساس گفته‌های بالا تابع مستقل از زمان قابل تعریف است..
[ویرایش] نمایش‌های مختلف سری فوریه
[ویرایش] نمایش مثلثی
اگر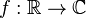 
یک تابع متناوب با دوره تناوب T باشد (یا به عبارتی: f(t + T) = f(t)) آنگاه این تابع را می‌توان به صورت زیر نوشت:
![f(t) = {a_0}+sum_{n=1}^{infty}[ a_n cos(omega_n t) + b_n sin(omega_n t)]](http://upload.wikimedia.org/math/e/f/4/ef409f7bcdc156b39dc547226e6a9c37.png)
که در آن ωn هارمونیک nام سری فوریه به رادیان بوده و ضرایب an، a0 و bn را می‌توان از فرمول‌های اولر بدست آورد.
فوریه بر این باور بود که هرگونه تابع متناوب را می‌توان به صورت جمعی از توابع سینوسی نوشت. این مطلب درست نمیباشد. شرایط لازم برای هر تابع متناوب برای اینکه به صورت سری فوریه نوشته شود به صورت زیر است:
- تابع در هر دورهٔ تناوبی انتگرال پذیر باشد:
- تابع فقط شمار محدودی بیشینه و کمینه دارد.
- تابع فقط شمار محدودی ناپیوستگی دارد.
[ویرایش] نمایش مختلط
سری فوریه می‌تواند به صورت زیر نیز نوشته شود:
و در اینجا:
.
این رابطه با کمک فرمول اویلر قابل گسترش به صورت زیر است:
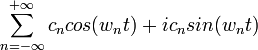
اگر این رابطه را به‌طور مستقیم با نمایش مثلثی مقایسه کنیم مشاهده میشود که cn به طریق زیر نیز قابل محاسبه است:
[ویرایش] نمایش کسینوس-با-فاز
نمایش زیر که در واقع شکل ویژه‌ای از نمایش مثلثی میباشد، نمایش کسینوس-با-فاز نام دارد. از این نمایش در رسم طیف خطی (به انگلیسی: line spectra) استفاده میشود.
[ویرایش] محاسبه ضرایب فوریه
[ویرایش] نمایش مثلثی
نمایش مثلثی بالا را در نظر بگیرید. همانطور که گفته شدT دوره تناوب و ωn هارمونی nام تابع میباشد. در تبدیل فوریه سه ضریب an و bn و ضریب ثابت a0 مطرح است. ضریب‌ها با استفاده از روابط زیر قابل محاسبه هستند.
بازه [π,π-] یا در کل بازه هایی که طول آنها 2π است از مهمترین بازه هایی است که درمحاسبه ضرایب استفاده میشود. بدین ترتیب p = 2π پس ضرایب عبارتند از:
نظرات شما عزیزان:
